为什么圆的面积的导数等于周长？球的的体积的导数等于其表面积？

圆的面积函数是

\[S(r) = \pi r^{2}\]

周长函数是

\[C(r) = 2\pi r\]

这二者的关系可以通过导数联系起来

\[S^{'}(r) = \left( \pi r^{2} \right)^{'} = 2\pi r = C(r)\]

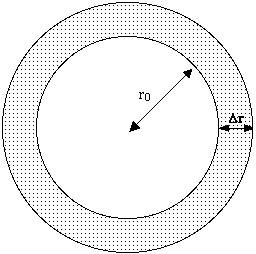
简而言之就是圆的面积的导数等于周长，为什么会这样呢？当半径增加\(\mathrm{\Delta}r\)时面积就增加\(\mathrm{\Delta}S\)——这可以视为增加了的圆环的面积，

¹

\(\mathrm{\Delta}r\)比较小的时候，增加的圆环的面积\(\mathrm{\Delta}S\)就近似等于长为\(2\pi r\)宽为\(\mathrm{\Delta}r\)的矩形的面积\(2\pi r \times \mathrm{\Delta}r\)。在求面积相对于半径的导数的时，要计算的是\(\frac{\mathrm{\Delta}S}{\mathrm{\Delta}r}\)的极限，而\(\frac{\mathrm{\Delta}S}{\mathrm{\Delta}r} \approx \frac{2\pi r \times \mathrm{\Delta}r}{\mathrm{\Delta}r} = 2\pi r\)，并且显然\(\mathrm{\Delta}r\)越小\(\frac{\mathrm{\Delta}S}{\mathrm{\Delta}r}\)和\(2\pi r\)就越接近，所以求\(\frac{\mathrm{\Delta}S}{\mathrm{\Delta}r}\)在\(\mathrm{\Delta}r \rightarrow 0\)情况下的极限得到的就是半径为\(r\)的圆的周长\(2\pi r\)。²

对于球体的体积和表面积也有类似的结论。球的体积函数是

\[V(r) = \frac{4}{3}\pi r^{3}\]

表面积函数是

\[A(r) = 4\pi r^{2}\]

这二者的关系可以通过导数联系起来

\[V^{'}(r) = \left( \frac{4}{3}\pi r^{3} \right)^{'} = 4\pi r^{2} = A(r)\]

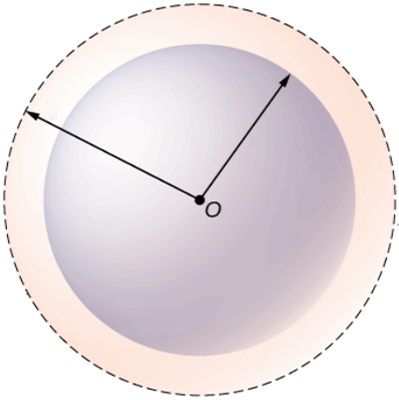
简而言之就是球的体积的导数等于表面积，为何如此？当球体半径增加\(\mathrm{\Delta}r\)时体积就增加\(\mathrm{\Delta}V\)——这可以视为增加了的球壳的体积，

³

\(\mathrm{\Delta}r\)比较小的时候，增加的球壳体积\(\mathrm{\Delta}V\)就近似等于底为\(4\pi r^{2}\)高为\(\mathrm{\Delta}r\)的柱体的体积\(4\pi r^{2} \times \mathrm{\Delta}r\)。在求体积相对于半径的导数的时，要计算的是\(\frac{\mathrm{\Delta}V}{\mathrm{\Delta}r}\)的极限，而\(\frac{\mathrm{\Delta}V}{\mathrm{\Delta}r} \approx \frac{4\pi r^{2} \times \mathrm{\Delta}r}{\mathrm{\Delta}r} = 4\pi r^{2}\)，并且显然\(\mathrm{\Delta}r\)越小\(\frac{\mathrm{\Delta}V}{\mathrm{\Delta}r}\)和\(4\pi r^{2}\)就越接近，所以求\(\frac{\mathrm{\Delta}V}{\mathrm{\Delta}r}\)在\(\mathrm{\Delta}r \rightarrow 0\)情况下的极限得到的就是半径为\(r\)的球的表面积\(4\pi r^{2}\)。